Multi-Objective

The following explains the details of the 4 multi-objective functions.

For multi-objective optimization, it is difficult to display the function form as in single-objective optimization. Therefore, we display the results of random sampling and the Pareto front line in a graph.

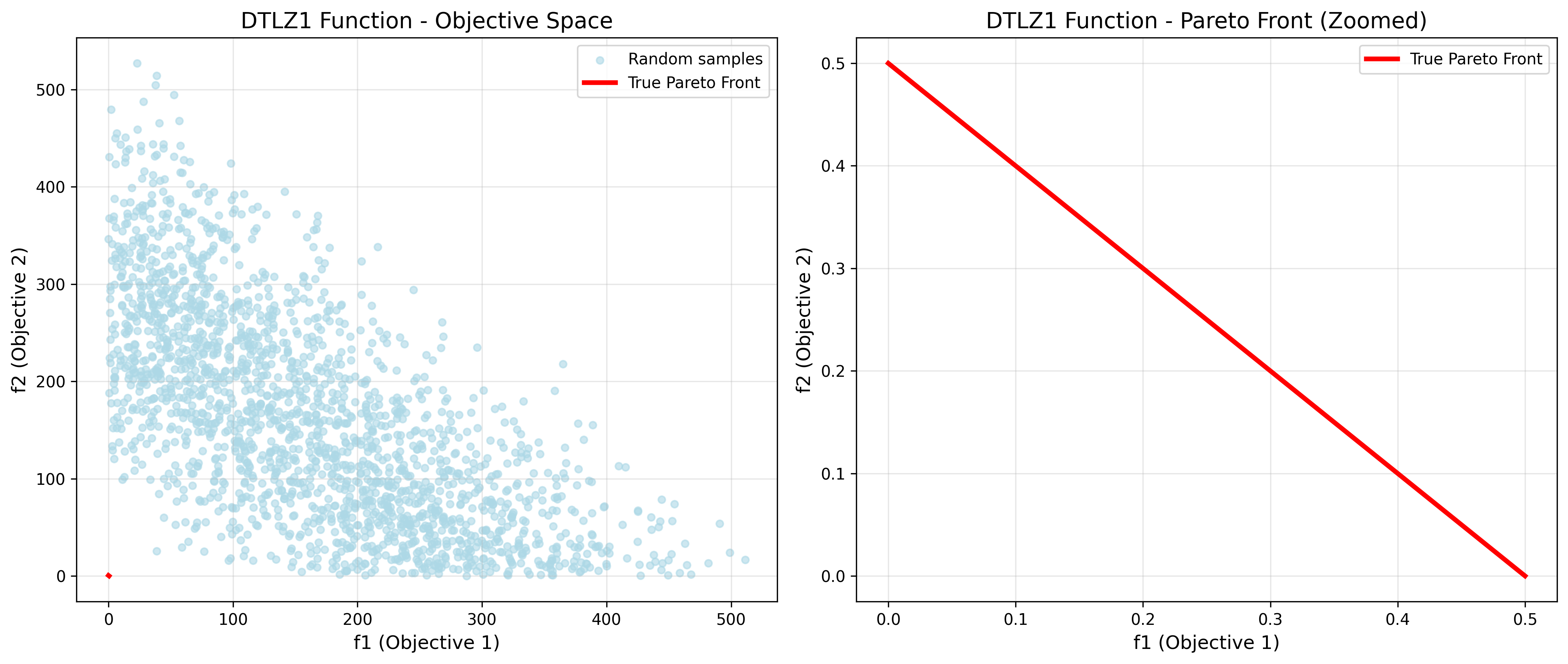
DTLZ1

DTLZ1 is a scalable multi-objective test problem featuring a linear Pareto front. This function is designed to test the convergence ability of multi-objective optimization algorithms in the presence of multiple local optima. It is particularly useful for evaluating algorithm performance on problems with linear trade-off relationships between objectives, such as resource allocation problems where different objectives compete linearly for limited resources.

Key characteristics:

• Linear Pareto front forming a hyperplane
• Multi-modal landscape with many local optima
• Scalable to any number of objectives
• Tests both convergence and diversity maintenance

$\begin{align} f_1(x) &= \frac{1}{2}x_1 x_2 \cdots x_{M-1}(1 + g(x_M)) \\ f_2(x) &= \frac{1}{2}x_1 x_2 \cdots x_{M-2}(1 - x_{M-1})(1 + g(x_M)) \\ &\vdots \nonumber \\ f_{M-1}(x) &= \frac{1}{2}x_1(1 - x_2)(1 + g(x_M)) \\ f_M(x) &= \frac{1}{2}(1 - x_1)(1 + g(x_M)) \\ &\nonumber \\ \text{where } g(x_M) &= 100[|x_M| + \sum_{x_i \in x_M}(x_i - 0.5)^2 - \cos(20\pi(x_i - 0.5))] \nonumber \\ \text{and } x_M &= \{x_M, x_{M+1}, \ldots, x_n\} \nonumber \end{align}$

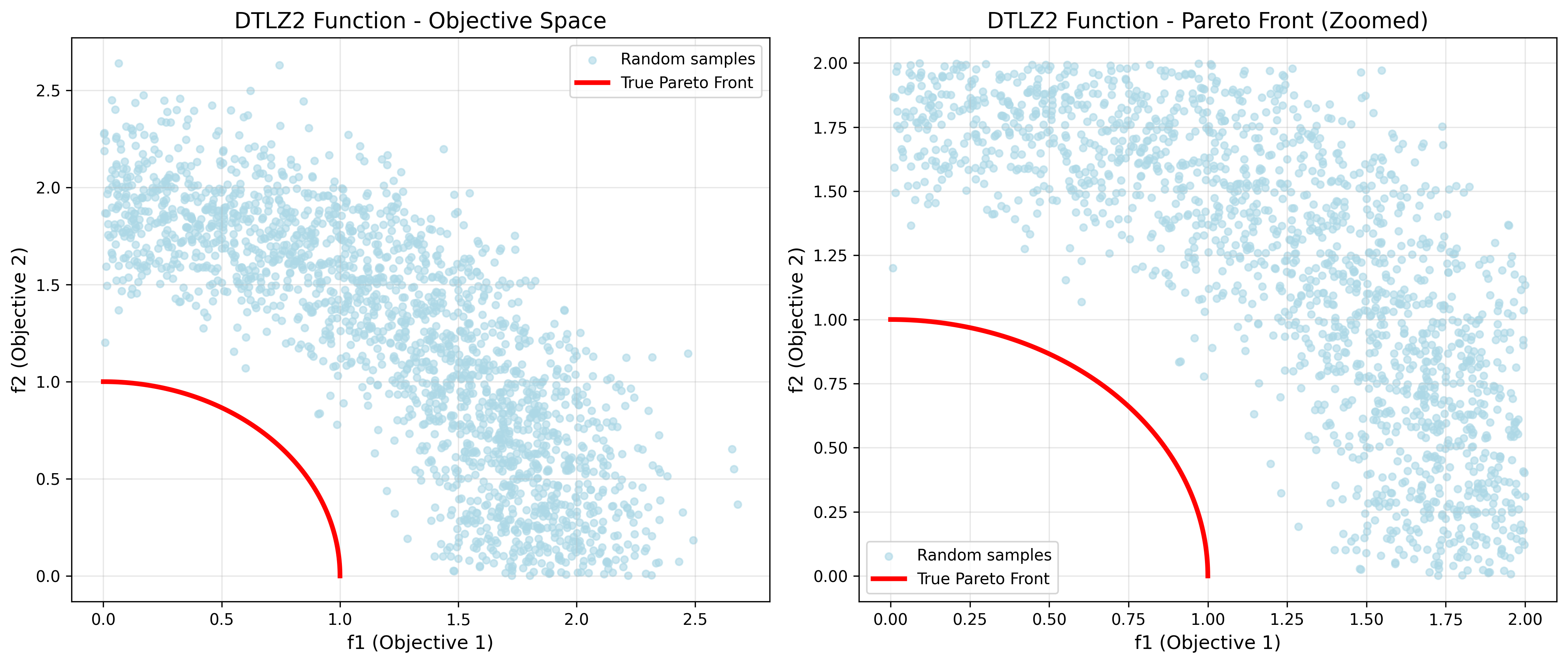
DTLZ2

DTLZ2 is a scalable multi-objective test problem with a spherical Pareto front. Unlike DTLZ1, this function has a unimodal structure, making it simpler but still challenging for testing algorithm convergence. It is designed to evaluate the ability of optimization algorithms to handle problems with spherical trade-off relationships, commonly found in engineering design where objectives represent different performance criteria with balanced trade-offs.

Key characteristics:

• Spherical Pareto front (unit sphere in objective space)
• Unimodal landscape (single global optimum region)
• Scalable to any number of objectives
• Ideal for testing convergence speed and solution quality

$\begin{align} f_1(x) &= (1 + g(x_M))\cos\left(\frac{\pi x_1}{2}\right)\cos\left(\frac{\pi x_2}{2}\right)\cdots\cos\left(\frac{\pi x_{M-1}}{2}\right) \\ f_2(x) &= (1 + g(x_M))\cos\left(\frac{\pi x_1}{2}\right)\cos\left(\frac{\pi x_2}{2}\right)\cdots\sin\left(\frac{\pi x_{M-1}}{2}\right) \\ &\vdots \nonumber \\ f_{M-1}(x) &= (1 + g(x_M))\cos\left(\frac{\pi x_1}{2}\right)\sin\left(\frac{\pi x_2}{2}\right) \\ f_M(x) &= (1 + g(x_M))\sin\left(\frac{\pi x_1}{2}\right) \\ &\nonumber \\ \text{where } g(x_M) &= \sum_{x_i \in x_M}(x_i - 0.5)^2 \nonumber \\ \text{and } x_M &= \{x_M, x_{M+1}, \ldots, x_n\} \nonumber \end{align}$

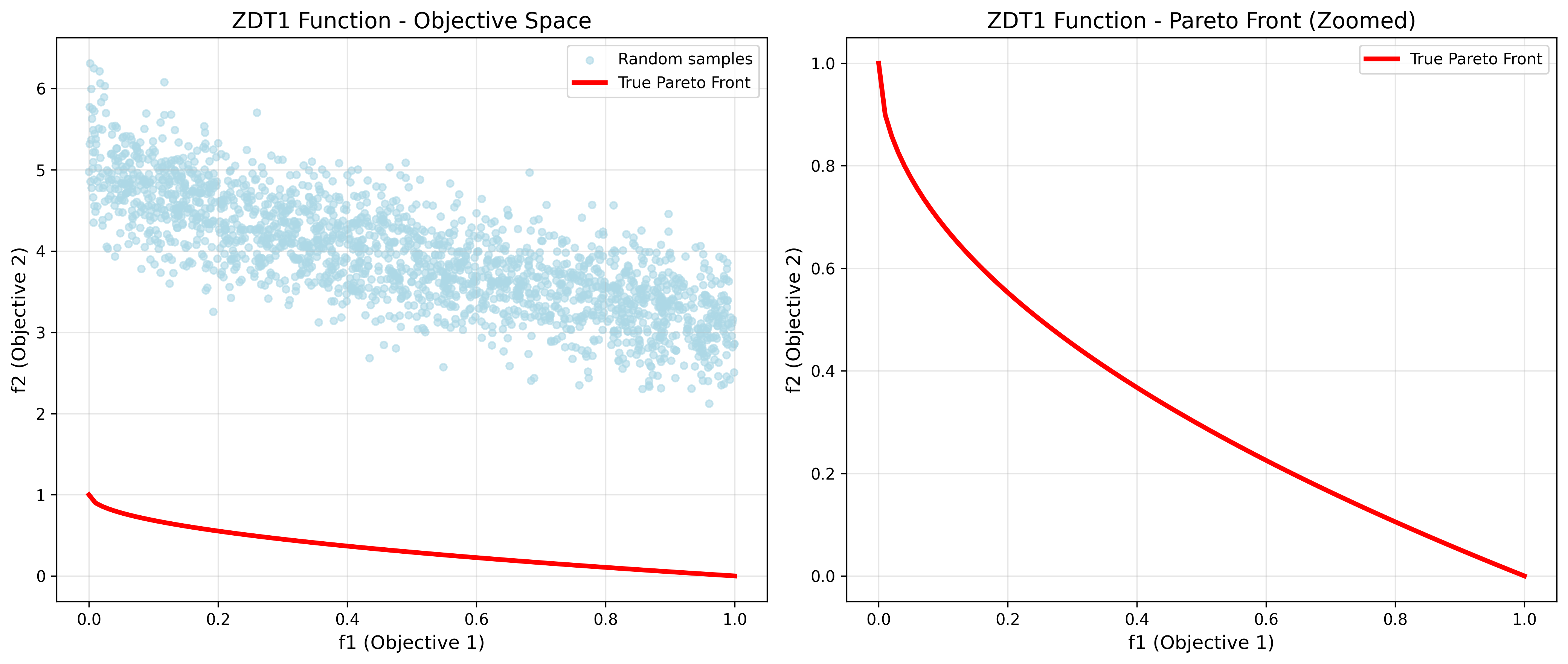
ZDT1

ZDT1 is a fundamental two-objective test function featuring a convex Pareto front. This function serves as a basic benchmark for bi-objective optimization algorithms and represents problems where objectives have a smooth, convex trade-off relationship. It is commonly used to test algorithm performance on problems similar to portfolio optimization, where risk and return exhibit convex trade-offs, or structural design where weight and strength follow convex relationships.

Key characteristics:

• Convex Pareto front with smooth curvature
• Two-objective formulation (f₁ vs f₂)
• Simple structure ideal for algorithm comparison
• Represents convex trade-off scenarios in real-world problems

$\begin{align} f_1(x) &= x_1 \\ f_2(x) &= g(x)\left[1 - \sqrt{\frac{x_1}{g(x)}}\right] \\ &\nonumber \\ \text{where } g(x) &= 1 + \frac{9}{n-1}\sum_{i=2}^{n}x_i \nonumber \\ \text{and } x_i &\in [0, 1] \text{ for } i = 1, 2, \ldots, n \nonumber \end{align}$

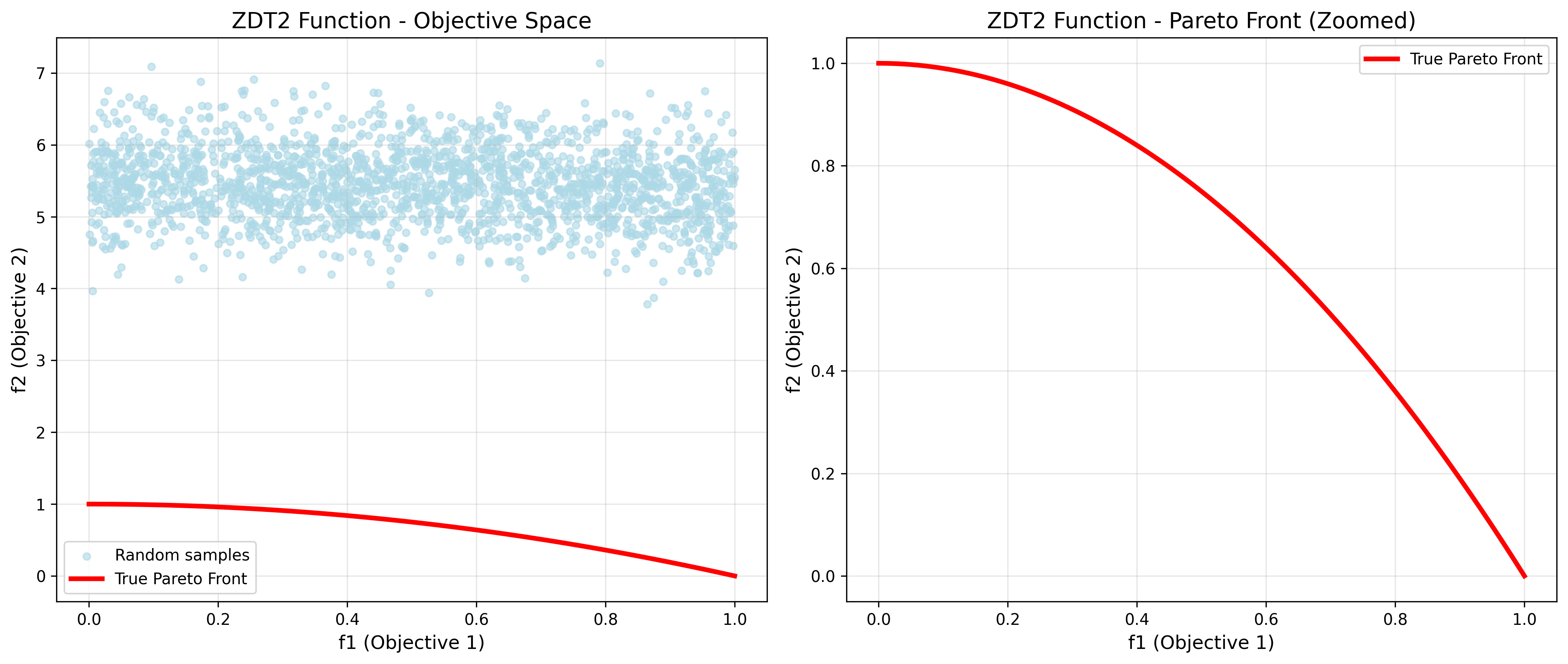
ZDT2

ZDT2 is a two-objective test function featuring a non-convex (concave) Pareto front. This function is designed to challenge optimization algorithms that assume convexity in the Pareto front shape. It represents real-world problems where objectives exhibit concave trade-off relationships, such as manufacturing processes where efficiency gains become progressively harder to achieve, or environmental problems where pollution reduction costs increase non-linearly.

Key characteristics:

• Non-convex (concave) Pareto front shape
• Two-objective formulation with increased complexity
• Tests algorithm ability to handle non-convex trade-offs
• Represents diminishing returns scenarios in optimization

$\begin{align} f_1(x) &= x_1 \\ f_2(x) &= g(x)\left[1 - \left(\frac{x_1}{g(x)}\right)^2\right] \\ &\nonumber \\ \text{where } g(x) &= 1 + \frac{9}{n-1}\sum_{i=2}^{n}x_i \nonumber \\ \text{and } x_i &\in [0, 1] \text{ for } i = 1, 2, \ldots, n \nonumber \end{align}$